-
手机版
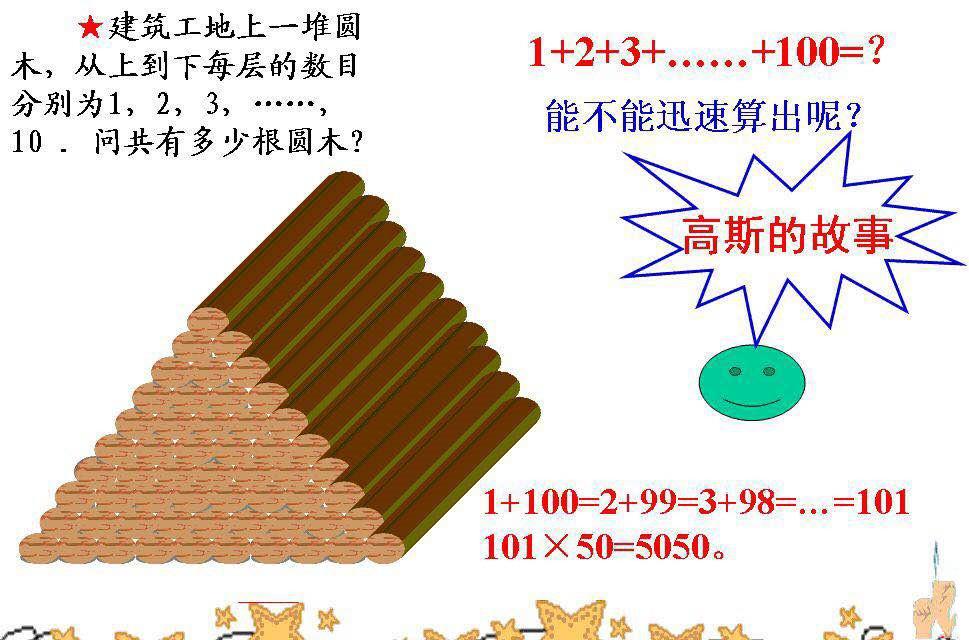
1.按照一定规律排列起来的一串数叫做数列,数列中的每一个数叫做一项,从左起第一个数叫做第一项,也叫首项;第二个数叫做第二项·····最后一个数叫做末项,数列里项的个数叫做项数。
2.一组数,如果从第二个数开始,每一项减去它紧邻前面的一项,所得的差都相等,具有这种特点的一组排列在一起的数列,叫做等差数列,每一项减去它的前一项所得的差叫做公差。
3.等差数列的基本公式:
等差数列的和=(首项+末项)×项数÷2;
公差=第二项-首项;
项数=(末项-首项)÷公差+1;
等差数列的第n项=首项+(n-1)×公差;
首项=末项-公差×(项数-1)。
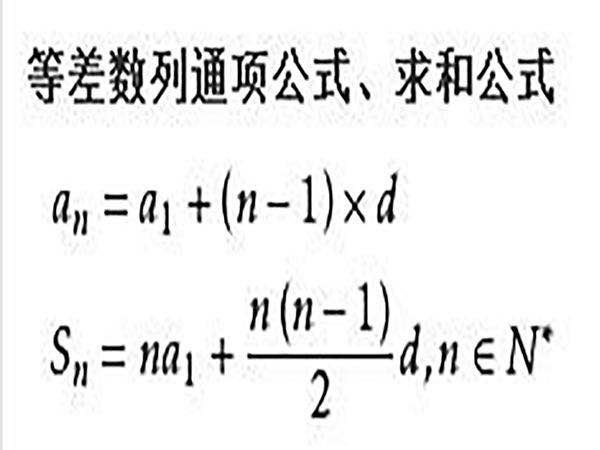
精讲1:计算(1+3+5+7+······+1997+1999)-(2+4+6+······+1996+1998)
分析:通过观察我们不难发现:前后两个括号里的数都是等差数列求和,因此可以先分别求出两个等差数列的和,再把两个和相减,通过观察比较容易发现:第一个括号里的等差数列公差为2,项数为1000项;第二个括号里的等差数列公差也为2,项数为999项。
解:(1+3+5+7+······+1997+1999)-(2+4+6+······+1996+1998)
=(1+1999)×1000÷2-(2+1998)×999÷2
=1000

精讲2:计算3+7+11+······+99
分析:题中所有加数是一个公差为4的等差数列,首项是3,末项是99,要求这个等差数列的和还必须知道项数:项数=(末项-首项)÷公差+1.求出了项数,我们就可以根据求和公式求出和。
解:项数为:(99-3)÷4+1=25
原式=(3+99)×25÷2=1275

精讲3:有60个数,第一个数是7,从第二个数开始,后一个数比前一个数多4,求这60个数的和。
分析:通过分析题意,我们知道:这是一个公差为4的等差数列,要求这个等差数列的和,必须知道首项、末项和项数。但题中只告诉了首项和项数,没有告诉我们末项,因此必须先求出末项,末项=首项+公差×(项数-1)。
解:末项为:7+4×(60-1)=243
60个数的和为:(7+243)×60÷2=7500
答:这60个数的和为7500。
精讲4:一个大礼堂 ,第一排有28个座位,以后每排比前一排多1个座位,第35排是最后一排,这个大礼堂共有多少个座位?
分析:从题中可以看出,大礼堂的各排座位数是一个公差为1的等差数列,求大礼堂共有多少个座位,实际上是求这个等差数列的和。已知首项是28,项数是35,第35排的座位数可以看成是末项,末项没有直接告诉我们,我们可以先求出末项,再求和。
解:末项为:28+1×(35-1)=62
35排共有座位数:(28+62)×35÷2=1575(个)
答:这个大礼堂共有1575个座位。

精讲5:把100根小棒分成10堆,每堆都是单数,一堆比一堆少2根,应如何分?
分析:根据题意可知这是项数是10,公差是2,数列和是100的等差数列。
解:设第十堆有x根,那么第一堆有x+(10-1)×2根,则:
{x+(10-1)×2+x}×10÷2=100
(2x+18)×5=100
2x+18=20
x=1
答:第十堆到第一堆分的个数分别是:1、3、5、7、9、11、13、15、17、19。