拉格朗日中值定理定义

下面是拉格朗日定理的具体定义：

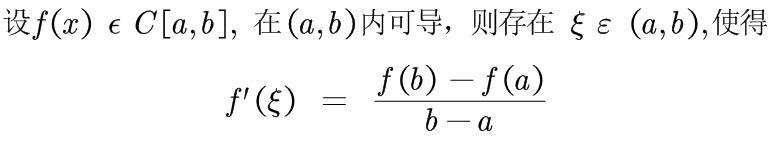
以下是其等价形式：

对其进行扩展，可得以下式子（端点变为变量）：

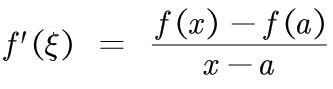
我们进行拆解，定理成立需要两个条件：

• f(x)在[a,b]上连续
• f(x)在(a,b)内可导

有以上两个条件，即可使用拉格朗日定理进行求解数学问题。

拉格朗日中值定理证明

证明此定理需要找一个辅助函数，怎么找呢？

首先，假设有曲线y=f(x)满足上述两个条件。

然后，另设一条直线经过(a,f(a)),(b,f(b))两点，那么其表达式为如下所示：

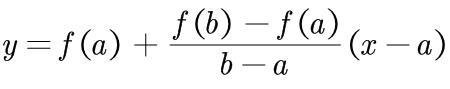
好了，那么我们的辅助函数呼之欲出：h(x)=曲线-直线，证明如图所示:

这里我们可以发现，当f(b)=f(a)时，拉格朗日定理变为罗尔定理。